본질적으로 파스칼의 법칙은 밀폐되고 비압축성인 유체의 어느 지점에서든 압력의 변화가 그 유체 전체에 걸쳐 동일하고 약화되지 않은 채 전달된다는 것을 말합니다. 이 원리는 유압 프레스의 기본 메커니즘으로, 작고 다룰 수 있는 힘을 엄청나게 강력한 힘으로 변환할 수 있게 해줍니다. 이는 초기 압력을 훨씬 더 넓은 영역으로 전달함으로써 결과적인 힘을 증폭시키는 방식으로 작동합니다.
파스칼의 법칙의 핵심 통찰은 공중에서 힘을 증폭시키는 것이 아니라는 것입니다. 대신, 비압축성 유체를 사용하여 압력을 균일하게 전달함으로써, 작은 면적에 가해지는 작은 힘이 더 큰 면적에 작용하는 동일한 압력을 생성하고, 결과적으로 더 큰 총 힘을 얻게 되는 것입니다.
파스칼의 법칙 해부하기
유압 시스템이 실제로 어떻게 작동하는지 완전히 이해하려면, 먼저 원리 자체의 세 가지 핵심 구성 요소를 이해해야 합니다.
압력의 정의
압력(P)은 특정 면적(A)에 가해지는 힘(F)으로 정의됩니다. 이 관계는 기본 공식인 P = F/A로 표현됩니다.
작은 면적에 집중된 작은 힘은 큰 면적에 걸쳐 퍼져 있는 거대한 힘과 동일한 압력을 생성할 수 있습니다. 이 개념은 힘 증폭을 이해하는 데 핵심적입니다.
비압축성 유체
파스칼의 법칙은 기름이나 물과 같은 비압축성 유체를 필요로 합니다. 이는 압력이 가해질 때 유체의 부피가 눈에 띄게 감소하지 않는다는 것을 의미합니다.
기체는 압축성이므로 압력 하에서 단순히 압축될 뿐 효율적으로 전달하지 못하므로 이 응용 분야에는 적합하지 않습니다.
약화되지 않는 전달
이것이 법칙에서 가장 중요한 측면입니다. 밀폐된 유체의 어느 부분에 압력을 가하든, 그 정확히 동일한 압력은 유체 내의 모든 곳에 즉시 전달됩니다.
물을 가득 채운 밀봉된 비닐봉지를 상상해 보십시오. 한 지점을 손가락으로 찌르면, 손가락이 있는 곳뿐만 아니라 봉지 전체가 팽팽해지고 압력이 고르게 증가합니다.
파스칼의 법칙이 유압 프레스를 작동시키는 방법
유압 프레스는 이 원리의 고전적인 실제 응용 사례입니다. 상당한 힘 증폭을 달성하기 위해 간단한 2개의 피스톤 시스템을 사용합니다.
2개의 피스톤 시스템
기본적인 유압 시스템은 비압축성 유체로 채워진 파이프로 연결된 두 개의 원통형 피스톤으로 구성됩니다.
- 피스톤 1 (입력): 작은 단면적(
A1)을 가집니다. - 피스톤 2 (출력): 훨씬 더 큰 단면적(
A2)을 가집니다.
작은 입력 힘(F1)이 피스톤 1에 가해져 유체 내에 압력을 생성합니다.
동일한 압력, 다른 힘
파스칼의 법칙에 따르면, 입력 피스톤(P1 = F1 / A1)에 의해 생성된 압력은 유체 전체에 걸쳐 약화되지 않고 전달됩니다. 이는 출력 피스톤(P2)에 작용하는 압력이 정확히 동일하다는 것을 의미합니다.
따라서, P1 = P2입니다.
P = F/A이므로, 이를 대입하여 다음 공식을 얻을 수 있습니다: F1 / A1 = F2 / A2.
힘 증폭 공식
방정식을 재배열하면 출력 힘(F2)에 대해 풀 수 있습니다:
F2 = F1 * (A2 / A1)
이는 증폭 효과를 우아하게 보여줍니다. 출력 힘은 입력 힘에 두 피스톤 면적의 비율을 곱한 값입니다. 출력 피스톤의 면적이 입력 피스톤 면적보다 100배 더 크다면, 힘은 100배 증폭됩니다.
상충 관계 이해하기
이 원리는 에너지를 공짜로 만들어내지 않습니다. 증폭된 힘은 대가를 치르게 되는데, 이는 에너지 보존 법칙에 의해 지배됩니다.
일의 보존
물리학에서, 일 = 힘 x 거리입니다. 유압 시스템이 평형 상태를 유지하려면, 입력 피스톤에 가해진 일이 출력 피스톤에 의해 수행된 일과 같아야 합니다.
Work_input = Work_output
F1 * d1 = F2 * d2
거리의 페널티
출력 힘(F2)이 입력 힘(F1)보다 훨씬 크기 때문에, 출력 피스톤이 움직이는 거리(d2)는 입력 피스톤이 움직이는 거리(d1)보다 비례적으로 더 작아야 합니다.
큰 피스톤으로 무거운 자동차를 1인치 들어 올리려면, 작은 피스톤을 몇 피트 밀어야 할 수도 있습니다. 힘 증폭을 위해 이동 거리를 교환하는 것입니다.
실제 비효율성
모든 실제 응용 분야에서 이상적인 출력 힘은 결코 완전히 달성되지 않습니다. 피스톤과 실린더 벽 사이의 마찰, 유체 점도, 시스템의 잠재적인 누출과 같은 요인들이 모두 힘 전달의 효율성을 약간 감소시킵니다.
목표에 맞는 올바른 선택하기
이 원리를 이해하면 주요 목표에 따라 목표 지향적인 설계 결정을 내릴 수 있습니다.
- 최대 힘 증폭에 중점을 두는 경우: 출력 면적(
A2)과 입력 면적(A1)의 비율을 최대화해야 합니다. - 작동 속도에 중점을 두는 경우: 더 높은 출력 거리(
d2)를 얻으려면 더 작은 면적 비율(A2/A1)이 필요하므로 낮은 힘 증폭 비율을 받아들여야 합니다. - 실제 시스템을 설계하는 경우: 비효율성을 위한 여유를 항상 고려해야 합니다. 마찰 및 기타 손실로 인해 실제 출력 힘은 이론적 계산보다 약간 적을 것입니다.
궁극적으로 파스칼의 법칙은 현대 기계 및 산업 공학의 초석으로 남아 있는 강력하고 우아한 프레임워크를 제공합니다.
요약표:
| 주요 측면 | 설명 |
|---|---|
| 파스칼의 법칙 | 비압축성 유체 내의 압력 변화는 유체 전체에 걸쳐 동일하고 약화되지 않은 채 전달됩니다. |
| 힘 증폭 공식 | F2 = F1 * (A2 / A1), 여기서 F2는 출력 힘, F1은 입력 힘, A2는 출력 면적, A1은 입력 면적입니다. |
| 상충 관계 | 힘이 증가하면 이동 거리가 감소하며, 이는 에너지 보존 법칙(F1 * d1 = F2 * d2)에 의해 결정됩니다. |
| 응용 분야 | 실험실의 유압 프레스에 이상적이며, 재료 테스트 및 처리를 위한 정밀한 힘 제어와 높은 효율성을 제공합니다. |
KINTEK의 첨단 유압 프레스 기계로 실험실 역량을 강화하십시오! 자동 실험실 프레스, 등압 프레스 또는 가열 실험실 프레스가 필요하든, 당사의 장비는 파스칼의 법칙을 활용하여 모든 실험실 요구 사항에 대해 정밀한 힘 제어, 높은 효율성 및 안정적인 성능을 제공합니다. 비효율성으로 인해 뒤처지지 마십시오. 당사의 솔루션이 재료 테스트 및 처리에서 생산성을 높이고 우수한 결과를 달성하는 방법을 알아보려면 오늘 문의하십시오!
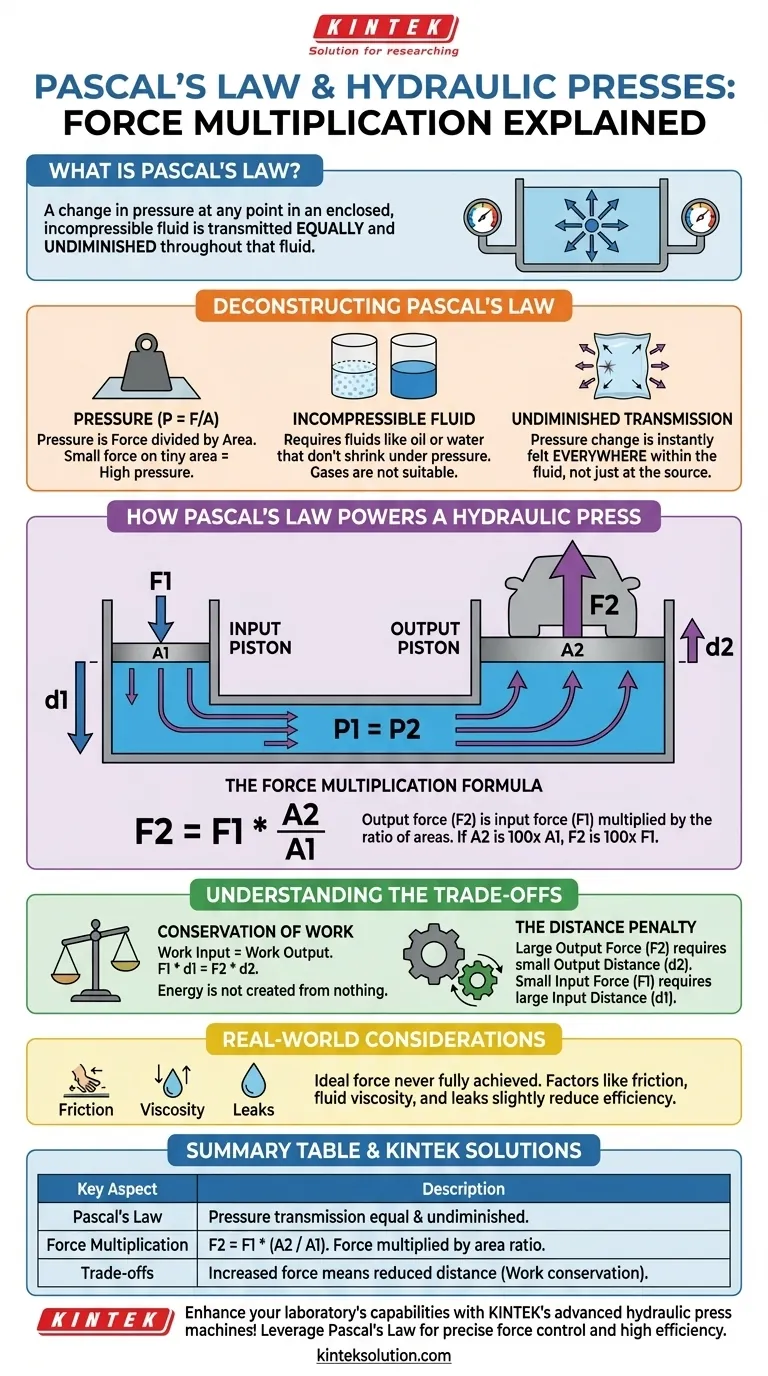
시각적 가이드
관련 제품
- 실험실용 유압 프레스 2T 실험실 펠릿 프레스 KBR FTIR용
- 실험실 유압 프레스 실험실 펠렛 프레스 버튼 배터리 프레스
- 자동 실험실 유압 프레스 실험실 펠렛 프레스 기계
- 핫 플레이트 유압 프레스 기계가 통합된 수동 가열식 유압 실험실 프레스
- 수동 실험실 유압 프레스 실험실 펠렛 프레스
